Effect of Environmental Precaution on the Transmission of Typhoid Fever: A Mathematical Modelling Approach
DOI:
https://doi.org/10.37134/ejsmt.vol12.1.10.2025Keywords:
Mathematical model, Basic reproduction number, Disease-free equilibrium, hygiene, global stabilityAbstract
We proposed and analyzed a nonlinear mathematical model for typhoid fever and optimal control in a community with overpopulation. The model considered the effect of environmental precautions on the transmission of typhoid fever. We obtained the basic reproduction number denoting the epidemic indicator. We proved the local and global asymptomatic stability conditions for disease-free and endemic equilibrium. The model exhibits strategies for optimal control of typhoid fever, such as preventive strategies (environmental sanitation, proper hygiene, vaccination) and the treatment strategy. The numerical simulation of typhoid fever disease transmission and its maximum control summarized that prevention and treatment are the best methods for eradicating the disease in society. Since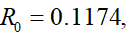 
which is less than one, it follows that the disease-free equilibrium is asymptomatically stable, and that the disease will always die out.
Downloads
References
J.W. Karunditu, G. Kimathi, S.Osman. (2019). Mathematical modeling of typhoid fever disease incorporating unprotected humans in the spread dynamics. Journal of Advance in Mathematics and Computer science, 32(3): 1- 11.
WHO (2007) Background paper on Vaccination against typhoid fever using new generation Vaccines. Presented at the SAGE meeting 11.
WHO (2021) Immunization Vaccines and biological. Available at https://www.int/teams/immuniztion - vaccines-and - biological /diseases/ typhoid.
J.K. Nihiiri, G.O. Lawi, C.O. Akinyi, D.O. Oganga, W.C. Muriuki, M.J. Musyka, P.O. Otieno, L. Koech.(2016). Mathematical modeling of typhoid fever disease incorporating protection against infection. Br. J. Math. Comput.Sci. 14(1); 1- 10.
J.M. Mutua, F.B. wang, N.K. Vaidya. (2015). Modeling Malaria and typhoid fever Co- infection dynamics. Math .Biosci. 264: 128- 144.
O.O. Temitope, M.O. Oluwatayo, N.O. Segun, E.F. Grace, O.O. Joshua, R.A. Opeyemi, Y.H. Omobolaji, O.O. Adenike . (2020). On the effect of vaccination, Screening and treatment in controlling typhoid fever spread dynamics deterministic and stochastic application. Math.Stat. 8(6): 621- 630.
M.N. Chamuchi, J.K. Sigee, J.A. Okello, J.M. Okwoyo. (2014) SIICR model and simulation of the effects of carriers on the transmission dynamics of typhoid fever in KISII town Kenya. 2014: 2(3).
O.J. Peter, M.O. Ibrahim, O.B Akinduko, M.Rabiu. (2017). Mathematics model for the control of typhoid fever. ISOR Journal of Mathematics 13(14)VerII: 60- 66.
O.D Makinde and K.O. Okosun . (2011). Impact of chemotherapy on optimal control of malaria disease with infected immigrants . Biosystems, 104(1): 32-41.
K.O Okosun and O.D. Makinde (2012). On a drug-resistant malaria model with susceptible individuals without access to basic amenities. Journal of Biological Physics, 38(3): 507-530.
K.O Okosun and O.D Makinde (2013). Optimal control analysis of malaria in the presence of non-linear incidence rate. Applied and Computational Mathematics. An International Journal, 12(1): 20- 32.
K.O. Okasun and O.D. Makinde. (2014). Optimal control analysis of hepatitis C virus with acute and chronic stages in the presence of treatment and infected immigrants. International Journal of Biomathematics, 7(2), Article ID 1450019, 23pp.
K.O. Okasun and O.D. Makinde. (2014). A Co- infection model of Malaria and Cholera diseases with optimal control. Mathematical Biosciences, 258: 19- 32.
World Health Organization (2000), Typhoid fever fact sheet ,http://www.who.int/mediacenter/factsheet/.
World Health Organization (2003), The Diagnosis, Treatment and prevention of Typhoid fever.
A. Alhassan, A.A. Momoh, S.A. Abdullahi and A. Audu. (2021). Mathematical Model for the Transmission Dynamics of Typhoid Fever Infection with Treatment. International Journal of Science for Global Sustainability, 7(2): 37- 49
Halson O. Nyaberi and Jane S. Musaili. (2021). Mathematical modeling of the impact of treatment on the dynamics of typhoid. 29(15): 1- 11.
E. Stephen and N. Nyerere. (2016). Modeling typhoid fever with education, vaccination and applied Mathematics. Am.J. Trop. Med.Hyg.2: 156- 164.
S. Muhayabasa, C.P. Bhunu, and N.A. Mhlanga. (2014). Modeling the Transmission Dynamics of Typhoid in Malaria Endemic Settings. An International Journal of Applications and Applied Mathematics (AMM), 9(1): 121-140.
H. Abboubakar and R. Racke. (2019). Mathematical Modeling and Optimal Control of Typhoid Fever. Downloaded from Konstanzer Online- Publication- System (KOPS); http://nbn-resolving.de/ 8(21): 352-367.
G.T. Tilahum, O.D. Makinde. (2017). Modeling and Optimal Control of Typhoid Fever Disease with Cost – Effective Straggles. Computational and Mathematical Methods in Medicine volume 2017: 1- 16.
O.J. Peter, O.A. Afolabi, F.A. Oguntolu, C.Y. Ishola and A.A Victor. (2018). Solution of a Deterministic Mathematical Model of Typhoid Fever by Variational Iteration Method. Science World Journal 13(2): 64- 68.
Oluwatobi, I. K., & Chris, L. A. (2023). Qualitative Analysis of the Transmission Dynamics and Optimal Control of Covid-19.
I.K. Oluwatobi, L.M. Erinle-Ibrahim (2021), Mathematical modelling of pneumonia dynamics of children under the age of five.
M. Erinle-Ibrahim Latifat, I.K. Oluwatobi, I. Sulola Abigail (2021), Mathematical modelling of the transmission dynamics of malaria infection with optimal control, Kathmandu Univ. J. Sci. Eng. Technol. 15.
A.C. Loyinmi, K.O. Idowu (2023), Semi-Analytic Approach to Solving Rosenau-Hyman and Korteweg-De Vries Equations Using Integral Transform, Tanzania J. Sci. 49: 26–40.
K.O. Idowu, T.G. Akinwande, I. Fayemi, U.M. Adam, A.C. Loyinmi (2023), Laplace Homotopy Perturbation Method (LHPM) for Solving Systems of N-Dimensional Non-Linear Partial Differential Equation, https://doi.org/https://doi.org/10.55810/2313-0083.1031.
E.-I.L. Morenikeji, A.O. Babajide, I.K. Oluwatobi (2021), Application of Homotopy Perturbation Method to the Mathematical Modelling of Temperature Rise during Microwave Hyperthermia, FUDMA J. Sci. 5:273–282.
Agbomola, J. O., & Loyinmi, A. C. (2022). Modelling the impact of some control strategies on the transmission dynamics of Ebola virus in human-bat population: An optimal control analysis. Heliyon, 8(12).
Erinle-Ibrahim, L. M., Adebimpe, O., Lawal, W. O., & Agbomola, J. O. (2022). A mathematical model and sensitivity analysis of Lassa fever with relapse and reinfection rate. Tanzania Journal of Science, 48(2), 414-426.
Agbomola, J., & Loyinmi, A. (2022). A Mathematical Model For The Dynamical Behavior Of Ebola Virus Transmission In Human-Bat Population: Implication Of Immediate Discharge Of Recovered Individuals.
Downloads
Published
How to Cite
Issue
Section
License
Copyright (c) 2024 Oluwatobi Kabir Idowu, Latifat Morenikeji Erinle-Ibrahim, Joshua Oluwasegun Agbomola, Sideeqoh Oluwaseun Olawale-Shosanya
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.
